To understand what’s important about the likely progress of the Covid-19 pandemic, there’s one key number you need to consider. That number is R, the number of new infections generated by each existing case. Whether R is greater than, or less than, or equal to 1 is a fundamental question.
If you answer that question wrongly, your modelling will get everything else wrong, no matter how careful you are with the details.
Unfortunately, or perhaps fortunately, the government’s expert advisers appear to be using the wrong answer, or at least they were in the modelling report released on Tuesday. That modelling, undertaken before we had experience of lockdowns, assumes that R will be greater than 1 even after we’ve locked down. This implies that the infection will keep spreading until it is limited by “herd immunity,” where so many people get infected that the growth rate has to finally slow, and R shrinks below 1.
But all the evidence, here and overseas, suggests that lockdowns push R below 1 regardless, which means the number of new cases declines over time. In the absence of a vaccine, that decline will be reversed if the lockdown is relaxed substantially, pushing R back above 1.
With smaller numbers of active cases, though, it should be possible to expand testing criteria to include all contacts of cases, whether or not they are symptomatic, and to undertake random testing, as is being done in Finland. This would provide better guidance on the stringency required for continuing controls.
The importance of R can be illustrated by the most familiar example of exponential growth, that of compound interest.
Suppose you invest $1000 and earn a 5 per cent rate of return. At the end of a year, you will have your original $1000 and a return of $50, meaning that R would equal 1.05. If you leave the interest to compound, after two years you will have $1050 plus the next year’s interest of $52.50, bringing your sum to $1102.50. And so on.
Suppose, however, that you simply put your money under the mattress. Then R would equal 1 and your $1000 wouldn’t grow.
Worse still, suppose that while your money sat under the mattress, prices were going up at an annual rate of 5 per cent. It would mean that after one year the purchasing power of your $1000 would have shrunk to $950 at the original price level. Over many years, with enough inflation, the value of your money would shrink to almost nothing.
This simple example illustrates the knife-edge property of R=1.
Of course, even with R greater than 1, exponential growth can’t go on forever without running into limits of some kind. In the case of an epidemic, the limiting factor is that, for most diseases, people who have been exposed and recovered acquire partial or complete immunity.
As this happens, R falls.
Suppose, for example, that each infected person passes the virus on to two others. R would equal 2. After a time, though, when half the population has been exposed, each infected person can only generate an average of one new infection, meaning R equals 1. After that, the infection rate will decline to below 1.
This “flattening the curve” graph released by the government illustrates the point. The uncontrolled case corresponds to R=2.53, estimated on the basis of the early stages of the Wuhan outbreak.
Social distancing (including lockdowns) is assumed to reduce R to between 1.69 and 1.9. Quarantine and isolation have a slightly more complex effect. The end result in the government’s publication is that, whatever measures are adopted, R stays above 1.
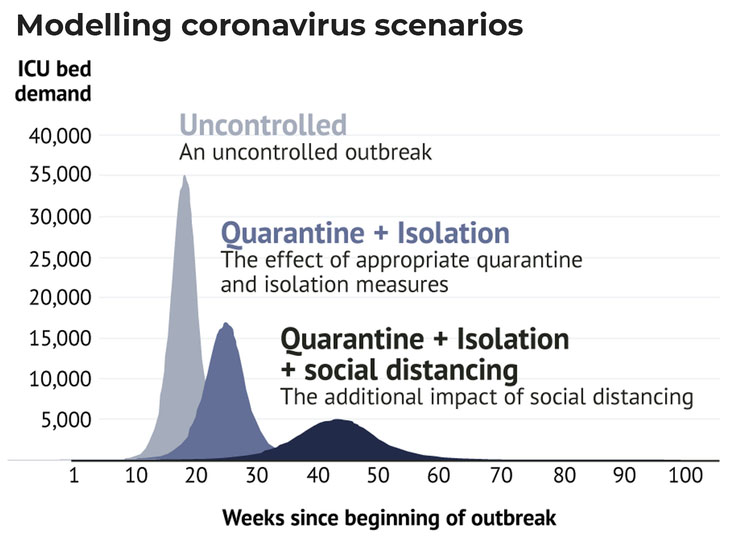
Source: Australian Government, Impact of Covid-19
What these assumptions mean is that the best thing we can hope for is to slow the spread enough for the hospital system to cope.
This is a gloomy picture, but it is important to recognise that modelling is an ongoing process and the official position is evolving. The research this week is based on early experience in Wuhan and does not incorporate evidence on the results of lockdown measures here or in other countries. So far, the decline in new infections suggests that stringent lockdowns are sufficient to push R well below 1 after only a few weeks.
Everywhere a sufficiently tight lockdown has been imposed, the number of new cases has peaked and declined long before herd immunity became relevant.
China used the most drastic measures and has reduced new cases to a trickle. South Korea (where statistics are more reliable) has done the same with more moderate restrictions. Even in European countries like Italy and Spain where the pandemic got out of hand before the controls were imposed, new cases have begun to decline.
For the moment, any problems with the government’s modelling don’t matter much. Whatever the value of R, it makes sense to maintain the existing lockdown measures for now.
But an assumption that R will stay above 1 might lead to ill-judged choices in the future, allowing a steady spread of the virus.
As New Zealand has made clear, our objective ought to be eradication. So long as R is less than 1, and extensive testing is used to control any outbreaks (locations or occupations in which R is greater than 1), there is no reason to think this is impossible. •




